MODALOGY - Ask the Modalogists: "Perfect Chords"

Buy Modalogy

Preview Modalogy

Modalogy Home

Modalogy Reviews

Ask the Modalogists

More Books

To submit a question, click here:

Perfect Chords

Type of stable chord that can "stand alone" in isolation without regard to either the previous or subsequent chord,
ie. without any harmonic or temporal reference.

·	All perfect chords (those built by stacking alternating quality thirds) are inherently stable, other thirds-stacking patterns are not.
·	The maximum number of notes in a perfect chord is 7.
·	All perfect chords can be derived from radially symmetric structures.
	·	The relative majors of perfect minor chords are also perfect.
	·	Supersets of perfect chords constructed by adding the alternate quality third to either end of the chord also results in a perfect chord.
	·	Preserving the root and select components, subsets of perfect structures also remain stable.

In addition to the perfect chords’ other attributes, the greater structures possess interlocking P5 pairs

1-5, 3-7, 5-9, 7-#11, 9-13

1-5, b3-b7, 5-9, b7-11, 9-13

The Perfect Chords

type 1

C major

|
C | E
M3
|

type 2

E minor

|
E | G
m3
|

type 1

Am7 & C6

|
A C | E G
m3 M3 m3
|

type 2

Cmaj7

|
C E | G B
M3 m3 M3
|

type 1

Fmaj9#11

|
F A C | E G B
M3 m3 M3 m3 M3
|

type 2

Am11 and
Cmaj13 (no 11)

|
A C E | G B D
m3 M3 m3 M3 m3
|

both type 1 and type 2

Dm13 & Fmaj13#11

|
D F A C | E G B D
|
m3 M3 m3 M3 m3 M3 m3
|

|
A C E G B D F# A
|
m3 M3 m3 M3 m3 M3 m3
|

Am13 & Cmaj13#11

"not" RS

min

A C E
m3 M3

maj

C E G
M3 m3

The minor / Major Dichotomy
The two primary and two secondary consonants
of the D centric pentatonic scale:

axis
|
a c | e g

A C E g

a C E G

a c | e g
|
axis

Of all the possible five chord roots in this RS pentatonic set,
only two are capable of producing a triad:

A (A C E) and C (C E G)

Minor Triad and Major Triad Combined

axis
			\|
R		b3	\|	3		5
	m3		h		m3
			\|
axis

"Relatively Stable" RS Chords

Out of all the 14 permutations of four stacked major and minor thirds (see addenda to this article), there are only two structures which possess radial symmetry:

The 9th chord and the mM9

The 9th chord

The RS stacking pattern {M3 m3 | m3 M3} forms the "dominant" 9th chord:

axis
\|
G		B		D		F		A
	M3		m3	\|	m3		M3
\|
axis

Although the harmonic series is not radially symmetrical itself (because it goes up and up and up), its lower harmonics generate a radially symmetrical structure (the 9th chord).

Along with the 9th chord’s RS and its intimate relationship with the natural harmonic series, it is also interesting because it has the complementary attributes of being capable of either acting as a force of tension for propelling forward circular motion [not stable] or simply remaining at rest [stable] (ie. its tritone can be regarded as either functional or non-functional [as with its little brother the 7th]).

The 9th chord may function as:

Dominant V (major & composite minor) / Secondary Dominant (V of x),

Or as the tonic of a mixolydian (for example).

Since this chord is not a member of the set of "perfect" chords, it is not categorized as "inherently" stable. Its dual nature prevents this anyway (unstable sometimes and stable sometimes).

The mM9 chord

When encountering the "mM7" as a final chord in a piece, many jazz musicians interpret that symbol to mean "play a mM9".

In Levine’s "Jazz Theory" book (pg 77), he states that the R b3 5 7 9 (aka "mM9") are the characteristic notes of the jazz minor.

The mM9 chord’s radial symmetry

axis
\|
G		Bb		D		F#		A
	m3		M3	\|	M3		m3
\|
axis

The mM9 chord (the 9th chord’s "mirror", eg. {M3 m3 | m3 M3} vs {m3 M3 | M 3 m3}) is also not a perfect chord, so it’s not "inherently" stable.

There is, without a doubt, some "clashiness" within this chord.

To many, the mM7 sounds harsher than the mM9. The presence of the 9th degree mellows out the clashes some.

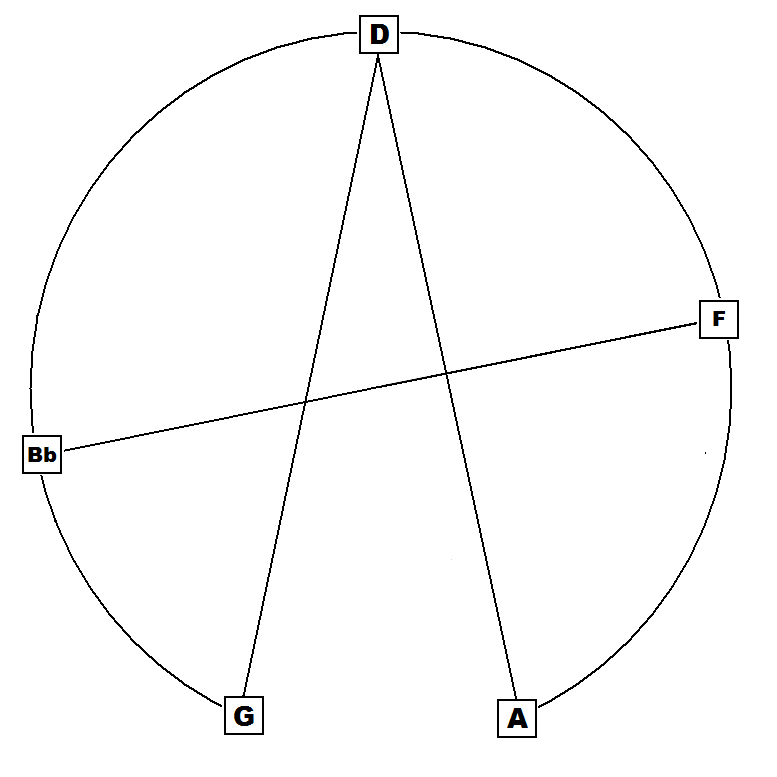
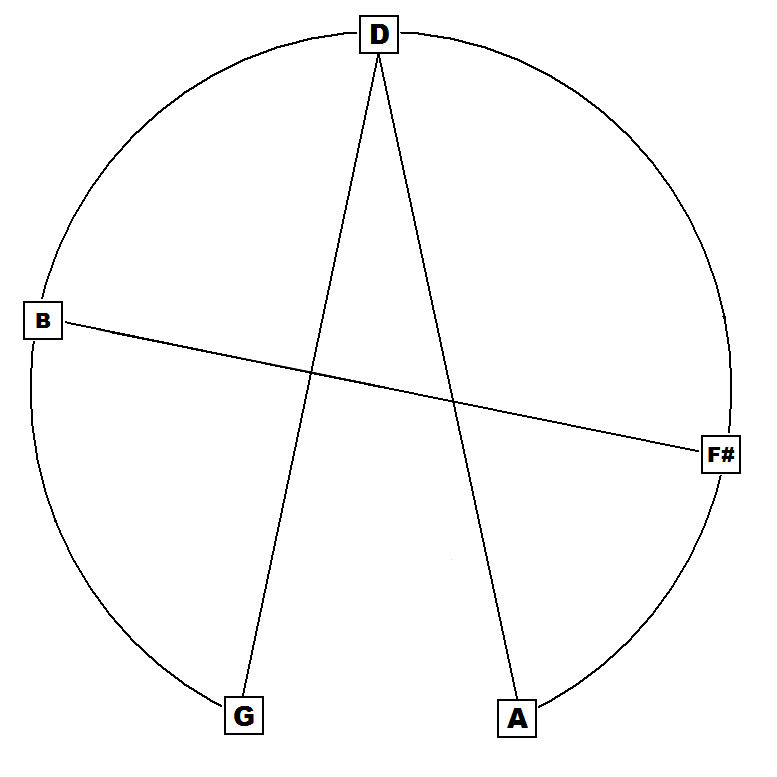
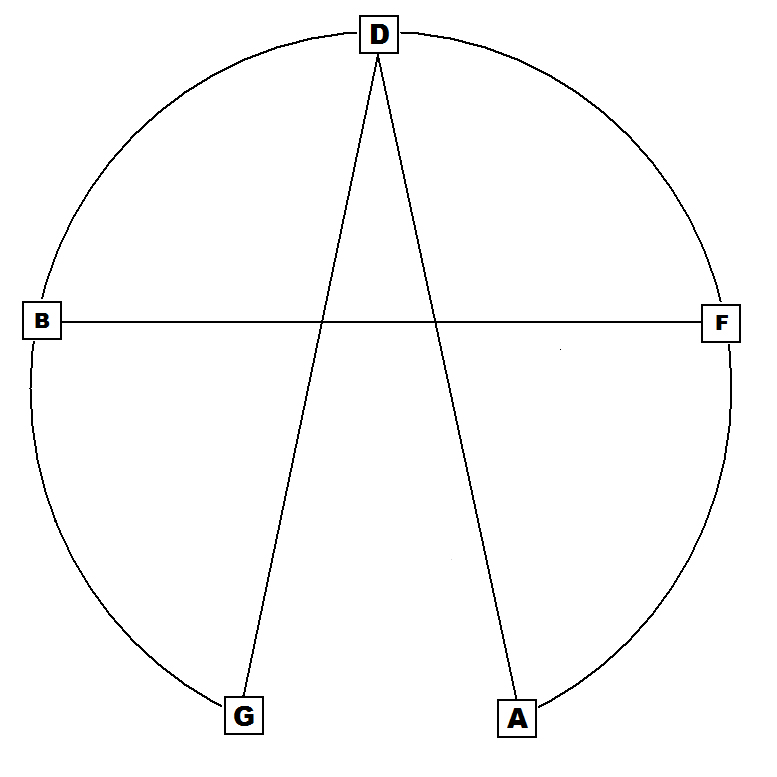
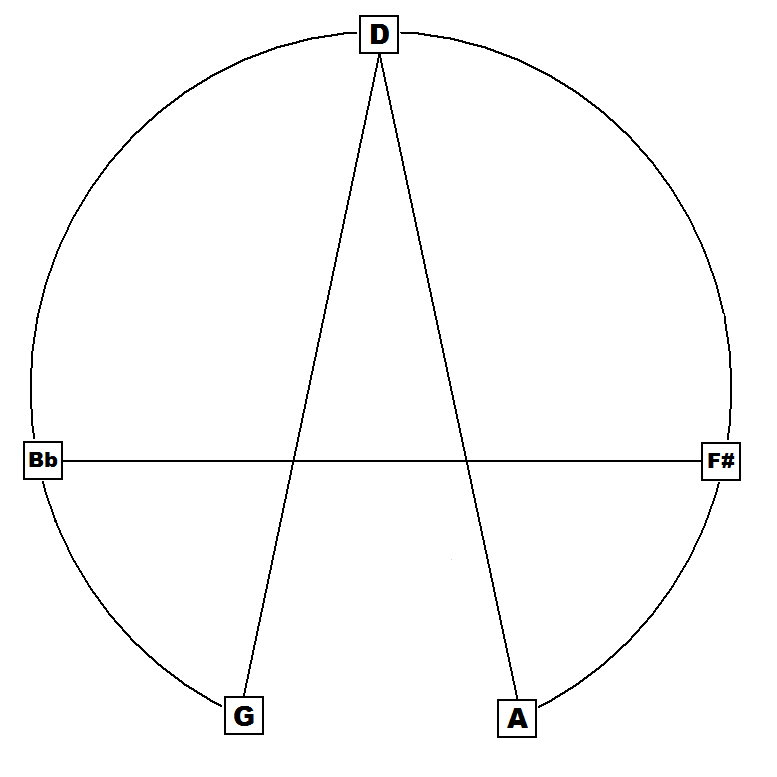
Both the 9th and mM9 chords can be described as radially symmetric mirrored triads,
conjoined and centered at D:

Dm
G

|
G B D F A
M3 m3 | m3 M3
|

GmM9

D
Gm

|
G Bb D F# A
m3 M3 | M3 m3
|

Compare:

G9 Dm G G B D F A M3 m3 m3 M3	Gmaj9 D G G B D F# A M3 m3 M3 m3
Gm9 Dm Gm G Bb D F A m3 M3 m3 M3	GmM9 D Gm G Bb D F# A m3 M3 M3 m3

Note the stable triads both top and bottom in all the above 4 structures.

The First Level RS Quintal

|
G D A
|

The central axis D note and its two primary consonants G and A (first level of radial symmetry) are constant in each of the four unique pentads analyzed here.

The unifying factor in this remarkable family of four-interval tertian chord structures is the two conjoined stacked P5s quintal.

The only variables are the permutations of the respective qualities of the thirds and sevenths that can be inserted into the underying stable quintal foundation.

axis
primary consonant	\|					primary consonant
G	D					A
\|	\|					\|
G		B	D	F		A
G	Bb		D	F		A
G	Bb		D		F#	A
G		B	D		F#	A
G		B	D	F		A
\|	\|					\|
G			D			A
primary consonant	\|					primary consonant
axis

None of the other "four-interval tertian pentads" exhibit these characteristics.

The radially symmetrical stable quintal formed by the two conjoined P5s (G-D | D-A) greatly contributes to the perceived relative stability of the 9th and mM9 chords.

Alternate Visualization

Stable Quintal Frame

Gm9

Gmaj9