Ask
the Modalogists
This is primarily a reference work for those interested in the quantum mechanics of music. Anyone wishing to fully explore the world of scales and their modes will find the most important issues dealt with in detail. Perfect for both music students and their teachers, as either a course in itself or to augment a music theory curriculum. There are also many sections of the book that directly relate to concepts and constructs confronted by jazz players: "Approach Tones", "Quartal Voicings", "Altered Chords", "The Minors", etc. Playing through the progressions on pages 17 thru 39 produces some amazing sonorities and voice motions for the composer/songwriter. The materials on pages 161 thru 191 are a bit more avant garde, but useful nevertheless in the right hands.
The
better command of the language you have, the more eloquently you can
express yourself.
After having thoroughly explored the minor and major pentatonics and their usage, the instructor can then move on to the 7-note natural diatonic sets of scales and modes (which is the ur-pentatonic scale plus two "new" notes, ie. the 3rd level of radially symmetrical consonance). In order to explore in detail the improvisational options inherent in the major scale and its modes, it is recommended for the teacher to play modal and tonal progressions on a rhythm instrument (piano, guitar) so that the student may improvise horizontally over them using the ionian/major, dorian, phrygian, mixolydian, aeolian and lydian modes (qv pgs 17-39). This entails illustrating a huge number of licks and tricks common to these various "moods", but in so doing the student REALLY gets to know their scales inside-out. It's a fun and real-world way to become intimately familiar with these extremely common and useful melodic devices.
Having wrapped up the study of horizontal improvisational techniques over the pentatonics and ionian set modes, naturally brings us to a study of the "composite" minor(s).The harmonic minor and melodic minor are introduced at this point. At the same time, the concept of borrowed parallel harmonies (both tonal and modal) can be covered.
This logical progression brings us to the study and use of non-tonal scales (wholetone, diminished, and modes of the ascending melodic minor, ie. the 4th, 5th and 6th levels of radially symmetrical consonance). It is at this juncture that the concepts of vertical soloing can enter the picture. This also coincides with the introduction of altered 7th chords into progressions.
The concept of the "Chromatic Cube" is an extension of the radially symmetrical principles laid out in the first half of the main text (noting relationships like the A B C# D E F G scale is the mirror of the A B C D Eb F G scale, and likewise the two diminished scales presented being mirrors of each other). The Cube is a really cool way to show how all the most commonly used scales in occidental 12TET (12-tone equal temperament) are interlocking, and that this crystalline entity is proof of how related and simple the basics of music really are.
The appendices cover common (and some uncommon) musical topics which are presented in an innovative, intuitive and useful manner for both the students' and teachers' easy reference.
Why is the analysis is based on the fourth, rather than the fifth? Perfect fifths radiating outward from the central D results in the identical pitch sets as radiating perfect fourths out does. Fourths were chosen for the convenience of having the initial triumvirat at the first level of consonance (A - D - G) fit within the space of one octave. If based on fifths, the first level triumvirat exceeds the octave as a M9 (G - D - A), which, when building scales, has to be octave adjusted anyway. Simply put, it saves a step.
No. Actually, there are several factors. In tertian progressions (tonal or modal), root motion is inarguably the most important mechanism that controls the forward or backward motion of the progression in relation to the intended tonic chord, but it is by no means the only factor determining the degree of any chord's relative cadential pull. Some cadences are stronger than others, and with good reason. Other factors, besides root motion, having influence on chords' cadential strength are chord quality, the presence of the characteristic note, and avoidance of the diminished triad (qv. pgs 17-18).
The authors discussed this issue at length and decided: 1. We wanted to keep the numbers of pages down to a reasonable figure (240 pages is the publisher's magic number). Adding in notation would increase the page count way beyond the 'sweet spot' - resulting in increasing the customer's price. 2. It is redundant to reiterate, via any representations such as guitar tablature or music staff notation, the same points that are otherwise already quite clearly explained within. 3. It is unnecessary to reprint sections from popular songs in order to "legitimize" the principles illustrated within. The concepts speak for themselves. 4. We also preferred to avoid the expense and potential for delays involved in securing copyright permissions for reprinting sections of current and well-known tunes (which may not be so well-known fifty years from now). There is no shortage of musical examples in the book, they just don't happen to be in staff notation. If you actually play through any of the musical materials within (scales, modes, progressions, etc), then, (assuming you've got soul) you'll immediately hear their musicality under your fingers. If you don't play through them, guranteed you won't hear anything. If there is any particular page or specific section of Modalogy that you would personally like to see written out in staff notation, tab, piano roll, neumes, parson's code, klavarskribo, braille, swaralipi, etc. feel free to "Ask the Modalogists".
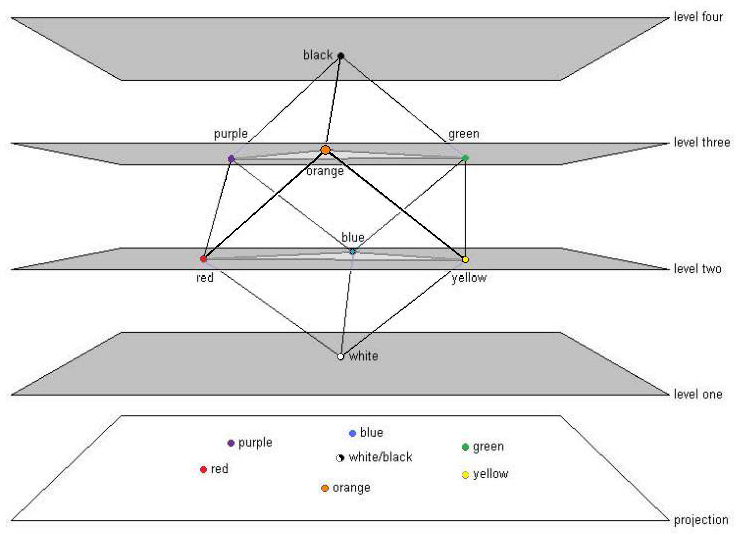
I Find Your Chromatic Cube To Be Very Fascinating. How Did You Coin That Concept? It evolved over a period of many years actually and has taken many forms. On page 78, you'll find a two dimensional representation which evolved from smaller parts. Note how the major scale and its modes 1 2 3 4 5 6 7 (ionian), 1 2 b3 4 5 6 b7 (dorian), etc... may be altered to produce melodic minor modes: #1 2 3 4 5 6 7 or 1 b2 b3 b4 b5 b6 b7 (altered dominant or superlocrian), 1 2 b3 4 5 6 7 (jazz melodic minor), etc... simply by raising one tone. Then the melodic minor may be altered by splitting the fifth: 1 2 b3 4 b5 #5 6 7 producing a diminished scale; or by extending its wholetone nature: #1 b3 4 5 6 7 the symmetrical aspect may be obtained by the exact same procedure as a mirror image: A B C D E F G becomes A B C# D E F G and A B C D E F G becomes A B C D Eb F G and so two melodic minors may be derived from but a single diatonic scale. Then each melodic minor may be split into their diminished and wholetone counterparts... as a diagram it kinda looked like this:
major
|
minor
/ \
diminished wholetone
and rather than "choosing" whether to raise the "1" or lower the "3" in the diatonic scale, I did both, not simply to preserve symmetry, but to keep my options open. The diagram you see on page 78 was completed by 2002, but it wasn't until the summer of 2005 that I realized that there was a three dimensional aspect that became the Chromatic Cube.
Fingering
Mastery
Why are colors associated with the scales of the Chromatic Cube?
The colors are simply descriptive labels (as are the letters of the alphabet for musical pitches). They are solely an aid towards visualization. The system of the Chromatic Cube required a means of being able to combine two labels in order to create a third label which still contained the properties of both the original labels. Color (it turns out) is the best and most intuitive system to satisfy these abovementioned requirements: RED
+ BLUE = PURPLE,
etc.
1. Unified The Chromatic Cube is a closed system governed by rules which create inherent limiting factors, ie. it is unified, a unity. 2. Field Three elements must be present to constitute a field: Space, Energy and Matter. No one of these three elements may be absent. In the chromatic cube, "space" is the Cube itself. "Space" is the glue that holds things together. Or more accurately, space is the glue that holds things APART. Space keeps Matter apart, yet still allows the flow of Energy In the chromatic cube, "matter" is the points of the Cube. The eight occidental scales are the matter. The flow of energy is the alterations effected that permit one scale to become another scale on any of the three points along its adjoining linear edges. Energy is measured in the distance from the origin, where White (the origin / natural scale) is the the state of least energy ("ground state"), the most consonant.
- Red, Blue and Yellow have a distance of 1 level higher energy - the next highest energy level: Green, Orange and Purple have a distance of 2 levels - the highest energy state exhibited in the chromatic cube is Black, a distance of 3 levels.
12-tone equal temperament, type 1 radial symmetry, and the presence of the two tritone components (essential tones) in every one of the eight scales.
"I recently bought Modalogy. I find the book fascinating. I noticed that the chromatic modes that appear in the book are for the Ionian mode/major scale. Could one also develop chromatic modes for harmonic/melodic minor, harmonic major or any other scale, and are these other chromatic modes commonly found in jazz or other styles of music?" In short, yes and yes. Chromatic Modes is a term developed to keep track of certain types of "outside" playing, mostly found in jazz but not necessarily; in other words, they may be applied to any type of music. Larry Carlton and the Brecker brothers are known for this kind of "stepping out," such as skating around the B major scale (C# dorian) as a means to provide tension in a Dm7 (Cmajor or D dorian) melody. This would be an example of mode bIII, with the tonal center D being embellished by the B major scale... Chromatic Modes may be applied to any scale or pitch collection. The use as described in Modalogy is meant for the set of scales defined as the Chromatic Cube (examples on pages 73 and 75) and as such, have already been applied to melodic minor (red and yellow) as well as harmonic major and minor (as subsets of the blue expansion)... However, the terms used in the book were proposed so that players such as yourself can begin to categorize and utilize these "extra-modal" events with some kind, any kind of "structure;" therefore, you may apply or otherwise rename them as you see fit.
All of the graphics are are perfectly logical and fully decipherable, practically representing a virtual Esperanto of Music. If you have a specific page with a graphic that you're having some trouble with and would like more explanation for, please contact us at "Ask the Modalogists". Or maybe just stare at it for a bit longer. One way or another, you'll definitely get it.
Modalogy is a reference work of scales and modes (and chords), just like the subtitle says, and by definition, reference works are supposed to be thorough. We have taken very simple and straightforward concepts, and produced a comprehensive summary of the most useful combinations of patterns (as well as much more). Most importantly, unique perspectives are presented that are not seen anywhere else (radial symmetry, chromatic cube, etc). Thanks for asking, but, no, 'Modalogy' isn't "just another" book.
Modalogy concerns itself with occidental scales and modes. It is not a study of world music, per se. Any treatise on Indian music should really be written by a master in the field. That being said, for those interested, here is a link to a thorough Analysis of Jairazbhoy's 32 Thaat Hindustani System.
In the primordial harmonic ooze there are two fundamental motions which represent ascending a fourth: V > I and I > IV Since the harmonic series breaks down at the 11th and is no longer musically useful, only the first 10 harmonics are used. With our fundamental at (say) A110, those first 10 harmonics form the A9 chord: { A C# E G B } (or arranged scalarly) While there are 5 notes in this pitch set, it is not our familiar "The Pentatonic Scale" that we all know and love. Rather it is a dominant quality chord/scale.
It is well known that the b7 of the harmonic series is considered "soft". However, (relative to A) the narrow tritone interval between the 5th harmonic (C#) and the 7th harmonic (G), as well as the wide tritone interval (h7=G to h10=C#) still fall within the boundaries of tritones used in historical tunings . This means that the tritone inherent in the harmonic series has tendency Should you wish to verify that fact, tune two guitar strings to a natural harmonic series tritone and listen. Whether Narrow or Wide - you will feel the tritone's need to resolve. The 5-note pitch set But which two? The two notes that the tritone components point to: C# points up to D, and G points down to F#.
D and F# are the two defining notes of the D major triad. Due to the tritone inherent in the harmonic series, playing a single A note on a musical instrument strongly implies a tendency to move up a fourth to a D (root or major triad). This explains why the strongest movement is for the V to move up to the I, AND it explains why, statistically, the IV chord is the very most common 2nd chord in a piece!
Introducing those two 'implied' notes the D and the F# into the { A B C# E G A } set, produces the (dominant flavored) heptatonic mixolydian scale { A B C# D E F# G A } DaRules Root motion is the most important factor in any chord progression, and the strongest and most common root motion is to go up a fourth - this is due to the tritone inherent in the harmonic series.
Not forgetting that the narrow tritone generated by the harmonic series is "soft", the explanation is simple: Any given note has two "tendencies": · To stay put · To move The "soft tritone" is only mildly "restless". This explains why a Blues can end on a dominant seventh, yet still feel at rest.
No, it is complementary. Playing a solitary A note out-of-the-blue can certainly feel as if we are "home" with no need to move. However, if the A note should move, its very strongest tendency is to move up a fourth to the D.
To submit a question, click here.
MODALOGY.NET |